2進数から10進数に基数変換！攻略法を教えます　ー離散数学ー

ITパスポートの入門と言ったら離散数学いわゆる2進数や10進数のことです。

2進数や10進数と聞いて頭を抱えているあなたに

離散数学を理解できるように説明していきます。

2進数や10進数、基数変換の攻略法を教えます！

そして、下に紹介している本は私が使っている本でとても読みやすいです。

私の記事を見ながら本を見るとより理解しやすくなるのでオススメです。

【改訂3版】ITパスポート最速合格術 ~1000点満点を獲得した勉強法の秘密 (情報処理技術者試験) 新品価格 ￥1,598から (2018/5/21 21:43時点)

2進数と10進数とは

10進数とは普段私たちが使用している数のことで、

0〜9の10種類の数字を使い、9の次は桁を上げるという表現技法が用いられています。

2進数は0〜1の2種類の数字を使い、1の次は桁を上げるというものです。

 

なぜ、2進数がコンピューター上で使われるのか？

コンピューターの中データは「電気が流れる、流れない」などの2つで作られるので

私たちが普段使っている10進数よりも2進数で表す方が適しているからです。

電気信号を数字に置き換えると「0」が電気が流れていない、「1」が電気が流れている、となります。

 

基数変換〜相互変換〜

まず、基数とは数字を表す時の桁上がりの基本となる数のことです。

簡単にいうと、２進数の基数は２、１０進数の基数は１０ということです。

ということは、基数変換は10進数を2進数に2進数を10進数に変換する問題のことを指します。

次からは実際に解き方を書いていきます。

 

2進数から10進数に変換

まず「（）_２」は2進数を表すときに使われる書き方です。

また10進数の場合は、「（）₁₀」という書き方になります。

なので数学が苦手というあなたのために文字に置き換えると、

例題は「2進数の101011.1101を10進数に変換してください。」となります。

 

表記の仕方もわかったところで本題に入っていきます。

2進数を10進数に変換する方法

2進数から10進数にするにはかけ算を使います。

言葉で説明すると、

整数部分は下の桁から順に2の0乗、1乗、2乗・・・と乗算を行い、

小数部分は上の桁から順に2の0乗、1乗、2乗・・・と乗算を行い、それを加算する。

という方法になりますが、こんな言い方されてもわからない！

というあなたのために整数部分、小数部分に分けて計算式を書いていきます。

 

整数部分だけを順に計算

まずは「101011」と並べます。

そして数字1つ1つに2をかけ算しますが、

その数字にかける「2」には乗数がくっつきます。

どのようにくっつくかというと下の桁から1,2,3,4,5、言い換えると

１の位は2の0乗

10の位は2の1乗

100の位は2の2乗、、、、、となり、それをかけ算すると下の画像のようになります。

一番左の「1」は10万の位、言い換えると、1の位を「0」として数えると5番目の位なので、

１×２^５＝32となります。もっと簡単に表すと、１×（２×２×２×２×２）＝32です。

左から2個目は「0」なので何をかけても「０」になるので、

０×（２×２×２×２）＝０となります。

以降同じ方法で計算していますので説明を省きます。

 

次に、出た答えまたは画像上の緑の丸に囲まれた部分を足し算してきます。

「３２＋０＋８＋０＋２＋１＝４３」

これが整数部分を２進数から10進数に戻した数となり、これで整数部分は終了です。

 

小数部分だけを順に計算

まずは「1101」と並べます。

そして数字1つ1つに2をかけ算しますが、

その数字にかける「2」には乗数がくっつきます。

ここまでは先ほどと同じですが、小数部分は乗数が「-」がつきます。

「２^-1」「２^-2」「２^-3」「２^-4」、、、、という表記になり、これらをかけ算してきます。

かけ算したのが下の画像です。見やすくするために画像サイズを大きくしています。

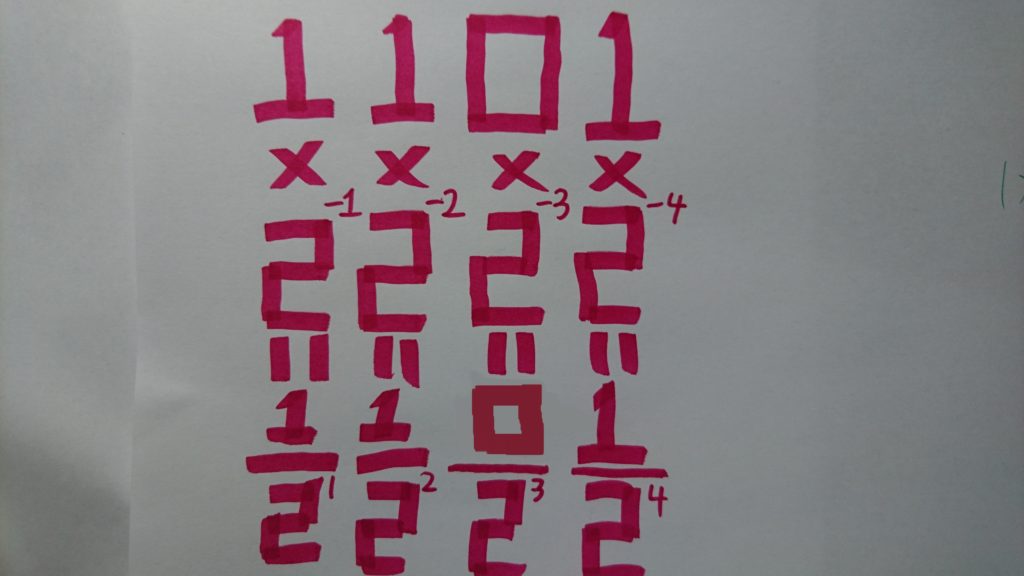
これで終わりではありません。

分数のままだと計算できないので、これ小数に直します。

 

すらすらと計算方法を説明しましたが、この一連を詳しく説明すると

まず乗数は小数点から近い順に数が小さくなっていきます。

一番左の「1」は小数点から一番近いので乗数が「-1」

左から2番目の「1」は小数点から数えて2番目なので乗数が「-2」

となり、それぞれ乗数のついた「2」をかけ算します。

画像ではいきなり、「1×2^-1」の答えが分数になっていますが、

深く考えないでください。理屈を考えようとするとキリがないので、

「1×2^-1」や「1×2^-２」という計算はまず乗数のマイナスが消えて分数になると覚えてください。

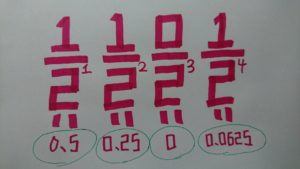
2枚の画像では分数がいきなり小数になっています。

これをわかりやすく説明すると、

「2¹分の1」は置き換えると「2¹」は「２」なので「1÷2」になるので答えは「0.5」

「2²分の1」は置き換えると「2²」は「2×2＝4」なので「1÷4」になるので答えは「0.25」

「2³分の０」は置き換えると「2³」は「2×2×2＝8」ですが「０÷8」になるので答えは「０」

「2⁴分の1」は置き換えると「2⁴」は「2×2×2×2＝16」なので「1÷16」になるので答えは「0.0625」となります。

 

最後に算出された答え（緑色の丸の数字）を足してください。

「0.5＋0.25＋0＋0.0625=0.815」となります。

これで小数部分の計算が終了しました。

 

まとめ

最後に、整数部分と小数部分をたすと

「43＋0.8125=48.8125」となり、これが2進数の101011.1101を10進数に変換した答えとなります。